最近一直在看“中国有嘻哈”这个综艺节目,通过这个节目听了一些嘻哈歌曲,了解了一些嘻哈文化,感觉还是挺有意思的。这个节目吸引人的地方有很多,除了嘻哈音乐本身,赛制过程中制作人和选手之间的diss,选手和选手之间的diss,粉丝和粉丝之间的diss也非常有趣。上周末结束的决赛也产生了足够劲爆的话题效果,竟然出现了双冠军。作为一个技术博客的开博之作,本文不讨论比赛中的黑幕等八卦消息,而是讨论下冠军产生过程中的概率问题。
冠军争夺战,在PG one和GAI表演结束之后,根据比赛规则,由100位Rapper评审和三组明星制作人共同投票选出最终的冠军。100位Papper评审每人1票,三组制作人每组拥有可以自由分配的50票,因此一共有250票。在节目上,让所有人惊叹的结果是,最终PG one和GAI以125票对125票的成绩打平,大家纷纷感叹小概率事件竟然发生了,节目中的字幕组给出了这个小概率事件发生的概率是$1.44\times 10^{-18}$,大概是10亿亿分之一。
这里不纠结到底是10亿亿分之一还是100亿亿分之一的问题,问题是这个概率真的有这么低吗?如果是这个概率,每年举办一次“中国有嘻哈”节目的话,平均也需要上亿亿年才能出现一次平票的情况,要知道地球的年龄也就大概45亿年,宇宙的年龄也就大概138亿年,亿亿年一遇的事情就这么巧被我们遇到了吗?
我们从概率论的角度分析一下。
简单情况
因为这个投票规则还是有些复杂的,先从相对简单的情况入手考虑一下,假如由250个人对两位选手投票,如果250个人的投票是完全随机的,那么有多大的可能性平票?
我开始回忆高中的排列组合知识来解决这个问题,按照高中时的解题套路,这个概率应该是个分式,分母是所有的投票可能情况,分子是所有平票的可能情况。
分母:
很简单,每个人只有2种选择,一共250个人,所以分母应该是$2^{250}$。
分子:
也不难,相当于在250个人中,选择125个人出来,投票给第一个选手,剩下的人投票给第二个选手,也就是$C_{250}^{125}$。
结果
因此,250个人随机投票取得平票的概率是:$$\frac{C_{250}^{125}}{2^{250}}\approx 0.05041$$
也就是说,有5%的可能性会平票,是不是比你想象中的大的多? 如果你被惊讶到了,那么这篇博客的目的就达到了:)
复杂情况
节目中的投票规则虽然是250票,但并不是250个人随机投票,因此和上面的简单情况不同。那么,如果按照节目规则,发生平票的概率是多少呢?
继续回忆高中的排列组合方法来求解:
分母:
每个Rapper手中只有1票,只有2种选择;每组制作人手中有50票,有51种选择(0 vs. 50, 1 vs. 49, … , 50 vs. 0)。因此分母是$2^{100}\times 51^{3}$。
分子:
分子的情况有些复杂,原谅我没有想出一个精妙的式子一下算出来,只能用笨办法分析。事实上,由于三组制作人手握150票,因此无论100个Rapper投出怎样的票型,只要三组制作人按照一定方式投票,最终都可以发生平票。假如100个Rapper的投票结果是(0 vs. 100),那么三组制作人的投票结果是(125 vs. 25)就可以平票了,也就是说,假如100个Rapper给A选手投了$r$票,三组制作人只要给A选手投($125-r$)票就会发生平票。
100个Rapper, A选手获得$r$票有$C_{100}^{r}$种可能。
三组制作人给A选手投$125-r$票有多少种可能呢?这是一个整数规划问题:$$x+y+z = 125-r, 0 \leq x,y,z \leq 50$$
这里我们假设这个问题有$f(125-r)$个解,我写了个程序求解函数$f(x)$,大概的结果是:$f(125)=f(25)=351, f(75)=1951$。
那么分子就可以计算了,共有$$\sum_{r=0}^{100} C_{100}^{r} f(125-r) $$种可能。
结果
将结果整理一下,假设三组制作人和100个Rapper随机投票,发生平票的可能性是: $$\frac{\sum_{r=0}^{100} C_{100}^{r} f(125-r)}{2^{100}\times 51^{3}}\approx 0.01452$$
也就是大约有1.45%的可能性会平票。
本文只是从概率论的角度,假设投票人完全随机投票,探讨了发生平票的可能性,仅供娱乐参考。
————————————————————————— 9.14 update —————————————————————————
“更复杂”的情况
看了下别的论坛,大家也都有讨论这个事情,有些同学说,“假设三组制作人随机投票是不对的!投0 vs. 50 这种票型的概率明显要小很多嘛!别以为我们读书少欺骗我们!”
我看到之后,感觉这些同学说的非常有道理,所以想考虑下这种情况下如何继续求解这个问题。但是我们仍需要进行一些假设才能求解。
三条假设
既然是决赛了,我们假设两位选手水平都比较高,因此这里给出三条假设:
- 对于100位Rapper,投给其中任何一个人的概率都是0.5;
- 对于制作人,投票的分数应该也是会比较接近的,0 vs. 50 或者 50 vs. 0 这种票型的概率应该很低。
我就找了一个和正态分布长的有些像的分布$p(x)$,这个分布大概形状如下图: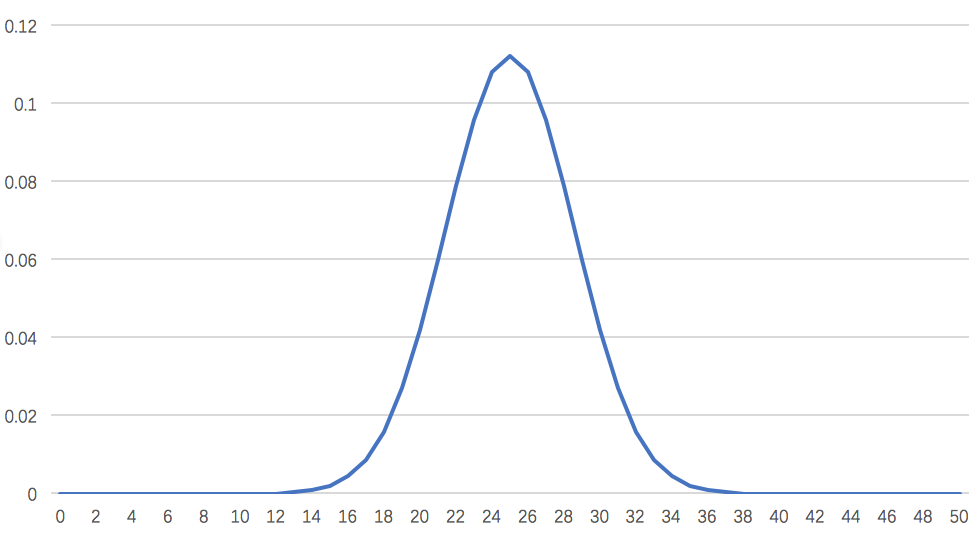
- Rapper评审和制作人之间的投票是相互独立的。
注意: 本节提出的假设和上一节“复杂情况”的假设事实上只有第二条假设不同,上一节假设制作人每种投票的概率都是1/51,而这里我们假设投票满足概率分布$p(x)$。
求解
在“复杂问题”那部分的求解过程基础上,这个问题的求解也不是很麻烦,只是把分子分母这种方法替换成概率就可以了。
对于100个Rapper, A选手获得$r$票的概率是$\frac{C_{100}^{r}}{2^{100}}$。
三组制作人给A选手投($125-r$)票的概率是多少呢?我们可以先求解整数规划问题:$$x+y+z = 125-r, 0 \leq x,y,z \leq 50$$
假设这个问题可行解的集合是$S(125-r)$,集合中的每个元素是一组$x,y,z$的取值。
那么三组制作人给A选手投($125-r$)票的概率等于:
$$F(125-r) = \sum_{(x,y,z) \in S(125-r)} p(x)p(y)p(z)$$
那么最终平票的概率就是:$$\sum_{r=0}^{100} \frac{C_{100}^{r}}{2^{100}} F(125-r)$$
结果
稍微修改一下程序(可以参考“代码实现”那篇博客),就可以计算出这种情况下平票的概率$\approx 0.05041$。发生平票的概率相比“复杂情况”变大了!
-
-
-
-
-
-
-
-
-
-
-
细心的读者可能发现了:“等等,这和你简单情况那一节的结果一样啊!”
哈哈,被你们发现了,原因就在于我选择的分布$p(x)$上,我选择的$p(x) = \frac{C_{50}^x}{2^{50}}$,数学名词叫二项分布,实际上就是假设随机投50次票,每次以0.5的概率投给A选手,最终A选手得x票的概率。这样一来,看似“更复杂”的情况就退化成了250个人随机投票的简单情况,当然结果是一样的了,是不是很有趣:)
当然,选择不同的分布$p(x)$,会使得最终的平票概率有所不同,我直观感觉,如果分布$p(x)$越平坦(最平坦就是第二节的情况),平票的概率越小;分布$p(x)$越尖锐,平票的概率越大,极端是制作人只会投平票,那么最终平票的概率相当于100个Rapper随机投票平票的概率,约等于0.07959。